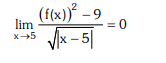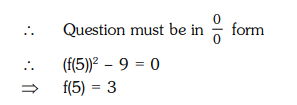Question: Let $f: \mathrm{R} \rightarrow[0, \infty)$ be such that $\lim _{x \rightarrow 5} f(x)$ exists and $\lim _{x \rightarrow 5} \frac{(f(x))^{2}-9}{\sqrt{|x-5|}}=0$. Then $\operatorname{Lim}_{x \rightarrow 5} f(x)$
equal -
Correct Option: , 3
Solution: