Question:
Mark $(\sqrt{)}$ against the correct answer in the following:
Let $f(\mathrm{x})=\left\{\begin{array}{r}\mathrm{x} \sin \frac{1}{\mathrm{x}}, \text { if } \mathrm{x} \neq 0 \\ 0, \text { when } \mathrm{x}=0\end{array}\right.$
Then, which of the following is the true statement?
A. $f(\mathrm{x})$ is not defined at $x=0$
B. $\lim _{x \rightarrow 0} f(x)$ does not exist
C. $f(\mathrm{x})$ is continuous at $\mathrm{x}=0$
D. $f(\mathrm{x})$ is discontinuous at $\mathrm{x}=0$
Solution:
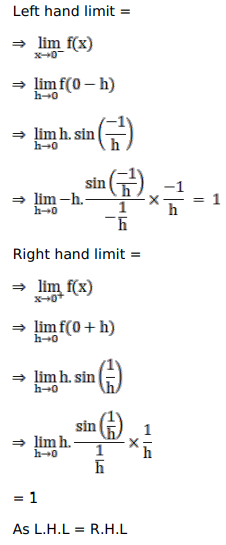
$\mathrm{F}(\mathrm{x})$ is continuous.
