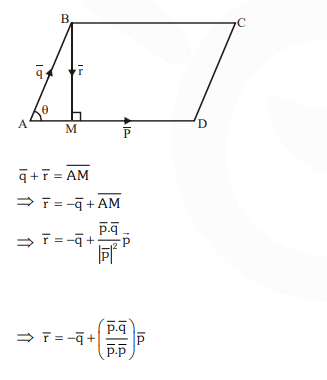
Question: Let $\mathrm{ABCD}$ be a parallelogram such that $\overrightarrow{\mathrm{AB}}=\overrightarrow{\mathrm{q}}, \overrightarrow{\mathrm{AD}}=\overrightarrow{\mathrm{p}}$ and $\angle \mathrm{BAD}$ be an acute angle. If $\overrightarrow{\mathrm{r}}$ is the vector that coincides with the altitude directed from the vertex $\mathrm{B}$ to the side $\mathrm{AD}$, then $\overrightarrow{\mathrm{r}}$ is given by :
$\overrightarrow{\mathrm{r}}=-3 \overrightarrow{\mathrm{q}}+\frac{3(\overrightarrow{\mathrm{p}} \cdot \overrightarrow{\mathrm{q}})}{(\overrightarrow{\mathrm{p}} \cdot \overrightarrow{\mathrm{p}})} \overrightarrow{\mathrm{p}}$
$\overrightarrow{\mathrm{r}}=3 \overrightarrow{\mathrm{q}}-\frac{3(\overrightarrow{\mathrm{p}} \cdot \overrightarrow{\mathrm{q}})}{(\overrightarrow{\mathrm{p}} \cdot \overrightarrow{\mathrm{p}})} \overrightarrow{\mathrm{p}}$
$\overrightarrow{\mathrm{r}}=-\overrightarrow{\mathrm{q}}+\left(\frac{\overrightarrow{\mathrm{p}} \cdot \overrightarrow{\mathrm{q}}}{\overrightarrow{\mathrm{p}} \cdot \overrightarrow{\mathrm{p}}}\right) \overrightarrow{\mathrm{p}}$
$\overrightarrow{\mathrm{r}}=\overrightarrow{\mathrm{q}}-\left(\frac{\overrightarrow{\mathrm{p}} \cdot \overrightarrow{\mathrm{q}}}{\overrightarrow{\mathrm{p}} \cdot \overrightarrow{\mathrm{p}}}\right) \overrightarrow{\mathrm{p}}$
Correct Option: , 3
Solution: