Question:
Let $a, b \in R$ be such that the function $f$ given by $f(x)=\ln |x|+b x^{2}+a x, x \neq 0$ has extreme values at $\mathrm{x}=-1$ and $\mathrm{x}=2$.
Statement-1 : $\mathrm{f}$ has local maximum at $\mathrm{x}=-1$ and at $\mathrm{x}=2$
Statement-2 : $\mathrm{a}=\frac{1}{2}$ and $\mathrm{b}=\frac{-1}{4}$.
Correct Option: , 3
Solution:
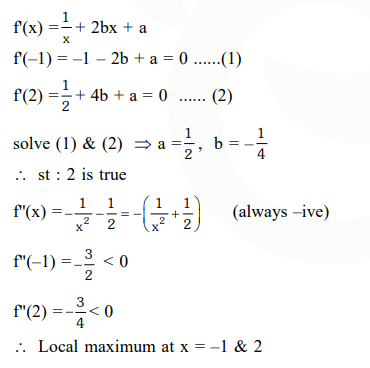
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
