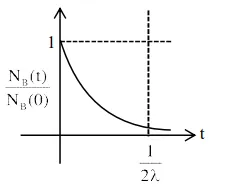
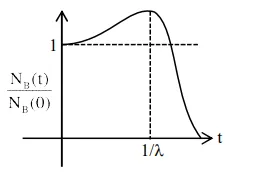
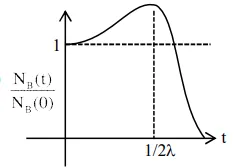
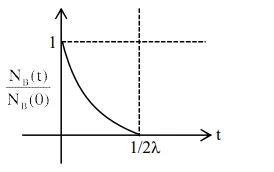
At time $\mathrm{t}=0$, a material is composed of two radioactive atoms $A$ and $B$, where $\mathrm{N}_{\mathrm{A}}(0)=2 \mathrm{~N}_{\mathrm{B}}(0)$. The decay constant of both kind of radioactive atoms is $\lambda$. However, A disintegrates to $B$ and $B$ disintegrates to $\mathrm{C}$. Which of the following figures represents the evolution of $\mathrm{N}_{\mathrm{B}}(\mathrm{t}) / \mathrm{N}_{\mathrm{B}}(0)$ with respect to time $\mathrm{t}$ ?
$\left[\begin{array}{l}\mathrm{N}_{\mathrm{A}}(0)=\text { No. of } \mathrm{A} \text { atoms at } \mathrm{t}=0 \\ \mathrm{~N}_{\mathrm{B}}(0)=\text { No. of } \mathrm{B} \text { atoms at } \mathrm{t}=0\end{array}\right]$
Correct Option: , 3
$\mathrm{A} \rightarrow \mathrm{B}, \mathrm{B} \rightarrow \mathrm{C}$
$\frac{\mathrm{dN}_{\mathrm{B}}}{\mathrm{dt}}=\lambda \mathrm{N}_{\mathrm{A}}-\lambda \mathrm{N}_{\mathrm{B}}$
$\frac{\mathrm{dN}_{\mathrm{B}}}{\mathrm{dt}}=2 \lambda \mathrm{N}_{\mathrm{B}_{0}} \mathrm{e}^{-\lambda \mathrm{t}}-\lambda \mathrm{N}_{\mathrm{B}}$
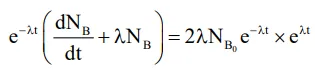
$\frac{\mathrm{d}}{\mathrm{dt}}\left(\mathrm{N}_{\mathrm{B}} \mathrm{e}^{\lambda \mathrm{t}}\right)=2 \lambda \mathrm{N}_{\mathrm{B}_{0}}$, on integrating
$\mathrm{N}_{\mathrm{B}} \mathrm{e}^{\lambda \mathrm{t}}=2 \lambda \mathrm{t} \mathrm{N}_{\mathrm{B}_{0}}+\mathrm{N}_{\mathrm{B}_{0}}$
$\mathrm{N}_{\mathrm{B}}=\mathrm{N}_{\mathrm{B}_{0}}[1+2 \lambda \mathrm{t}] \mathrm{e}^{-\lambda \mathrm{t}}$
$\frac{\mathrm{dN}_{\mathrm{B}}}{\mathrm{dt}}=0$ at $-\lambda[1+2 \lambda \mathrm{t}) \mathrm{e}^{-\lambda \mathrm{t}}+2 \lambda \mathrm{e}^{-\lambda \mathrm{t}}=0$
$\mathrm{N}_{\mathrm{B}_{\max }}$ at $\mathrm{t}=\frac{1}{2 \lambda}$