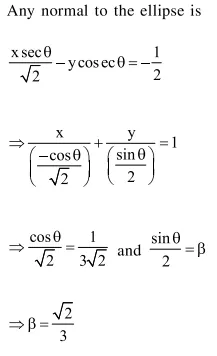Question:
Let the line $y=m x$ and the ellipse $2 x^{2}+y^{2}=1$ intersect at a ponit $\mathrm{P}$ in the first quadrant. If the normal to this ellipse at $\mathrm{P}$ meets the co-ordinate axes at $\left(-\frac{1}{3 \sqrt{2}}, 0\right)$ and $(0, \beta)$, then $\beta$ is equal to
Correct Option: , 4
Solution: