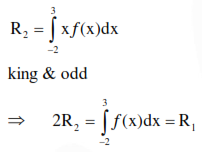Question:
Let $f:[-2,3] \rightarrow[0, \infty)$ be a continuous function such that $\mathrm{f}(1-\mathrm{x})=f(\mathrm{x})$ for all $\mathrm{x} \in[-2,3]$. If $R_{1}$ is the numerical value of the area of the region bounded by $y=f(x), x=-2, x=3$ and the axis of $\mathrm{x}$ and $\mathrm{R}_{2}=\int_{-2}^{3} x f(x) d x$, then :
Correct Option: , 4
Solution: