The angle of depression of a car, standing on the ground,

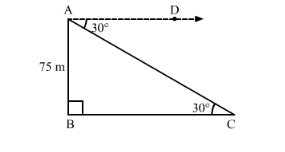
Suppose AB is the tower and C is the position of the car from the base of the tower.

It is given that, AB = 75 m

Now, $\angle A C B=\angle C A D=30^{\circ}$ (Alternate angles)

In right ∆ABC,

$\tan 30^{\circ}=\frac{\mathrm{AB}}{\mathrm{BC}}$

$\Rightarrow \frac{1}{\sqrt{3}}=\frac{75 \mathrm{~m}}{\mathrm{BC}}$

$\Rightarrow \mathrm{BC}=75 \sqrt{3} \mathrm{~m}$

Thus, the distance of the car from the base of the tower is $75 \sqrt{3} \mathrm{~m}$.

Hence, the correct answer is option C.