The angle of elevation of a cloud $C$ from a point $P, 200 \mathrm{~m}$ above a still lake is $30^{\circ}$. If the angle of depression of the image of $C$ in the lake from the point $P$ is $60^{\circ}$, then $P C$ (in $\mathrm{m}$ ) is equal to:
Correct Option: , 3
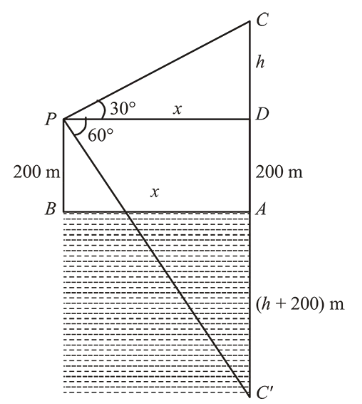
Here in $\triangle P C D$,
$\sin 30^{\circ}=\frac{h}{P C} \Rightarrow P C=2 h$......$\ldots$ (i)
$\tan 30^{\circ}=\frac{h}{x} \Rightarrow \frac{1}{\sqrt{3}}=\frac{h}{x}$
$\Rightarrow x=\sqrt{3} h$ ...(ii)
Now, in right $\triangle P C^{\prime} D$
$\tan 60^{\circ}=\frac{h+400}{x}$
$\Rightarrow \sqrt{3} x=h+400 \Rightarrow 3 h=h+400$[From(ii)]
$\Rightarrow h=200$
So, $P C=400 \mathrm{~m}$ [From (i)]
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.