The angle of elevation of a jet plane from a point $\mathrm{A}$ on the ground is $60^{\circ}$. After a flight of 20 seconds at the speed of $432 \mathrm{~km}$ / hour, the angle of elevation changes to $30^{\circ}$. If the jet plane is flying at a constant height, then its height is:
Correct Option: 1
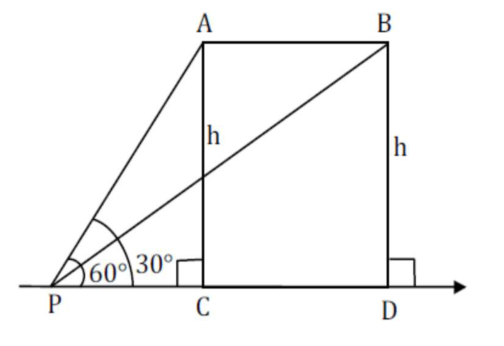
$v=432 \times \frac{1000}{60 \times 60} \mathrm{~m} / \mathrm{sec}=120 \mathrm{~m} / \mathrm{sec}$
Distance $A B=v \times 20=2400$ meter
In $\Delta \mathrm{PAC}$
$\tan 60^{\circ}=\frac{h}{P C} \Rightarrow P C=\frac{h}{\sqrt{3}}$
In $\Delta \mathrm{PBD}$
$\tan 30^{\circ}=\frac{h}{P D} \Rightarrow \mathrm{PD}=\sqrt{3} \mathrm{~h}$
$P D=P C+C D$
$\sqrt{3} h=\frac{h}{\sqrt{3}}+2400 \Rightarrow \frac{2 h}{\sqrt{3}}=2400$
$\mathrm{h}=1200 \sqrt{3}$ meter
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.