The angle of elevation of an aeroplane from a point on the ground is 45°.

Let angle of elevation of an aero plane is 45°. After 15 second angle of elevation is change to 30°. Let DE be the height of aero plane which is 3000 meter above the ground. Let , ,  and. Here we have to find speed of aero plane.

We have the corresponding figure as follows

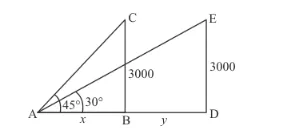
So we use trigonometric ratios.

In $\triangle A B C$

$\Rightarrow \quad \tan A=\frac{B C}{A B}$

$\Rightarrow \quad \tan 45^{\circ}=\frac{3000}{x}$

$\Rightarrow \quad 1=\frac{3000}{x}$

$\Rightarrow \quad x=3000$

Again in $\triangle A D E$

$\Rightarrow \quad \tan A=\frac{D E}{A B+B D}$

$\Rightarrow \quad \tan 30^{\circ}=\frac{3000}{x+y}$

$\Rightarrow \quad \frac{1}{\sqrt{3}}=\frac{3000}{3000+y}$

$\Rightarrow \quad 3000+y=3000 \sqrt{3}$

$\Rightarrow \quad y=3000 \sqrt{3}-3000$

$\Rightarrow \quad y=3000(\sqrt{3}-1)$

$\Rightarrow \quad y=2196$

Since $15 \mathrm{sec}=2196$

$\Rightarrow \quad \mathrm{sec}=\frac{2196}{15}=146.4$

$\Rightarrow \quad \sec =\frac{2196}{15}=146.4$

$=\frac{146.4 \times 3600}{1000}$

$=527.04$

Hence the speed of aero plane is $527.04 \mathrm{~km} / \mathrm{h}$.