The angle of elevation of the summit of a mountain from a point on the ground is $45^{\circ}$. After climbing up on $\mathrm{km}$ towards the summit at an inclination of $30^{\circ}$ from the ground, the angle of elevation of the summit is found to be $60^{\circ}$. Then the height (in $\mathrm{km}$ ) of the summit from the ground is:
Correct Option: , 3
$\because \angle D C A=\angle D A C=30^{\circ}$
$\therefore A D=D C=1 \mathrm{~km}$
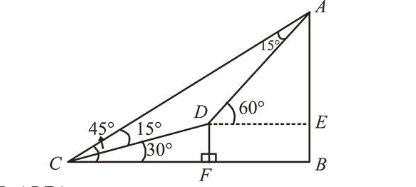
In $\triangle D E A$,
$\frac{A E}{A D}=\sin 60^{\circ} \Rightarrow A E=\frac{\sqrt{3}}{2} \mathrm{~km}$
In $\Delta C D F, \sin 30^{\circ}=\frac{D F}{C D} \Rightarrow D F=\frac{1}{2} \mathrm{~km}$
$\therefore E B=D F=\frac{1}{2} \mathrm{~km}$
$\therefore$ Height of mountain $=A E+E B$
$=\left(\frac{\sqrt{3}}{2}+\frac{1}{2}\right)=\left(\frac{\sqrt{3}+1}{2}\right) \mathrm{km}=\frac{1}{\sqrt{3}-1} \mathrm{~km}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.