The angle of elevation of the top of a tower is 30°.

False

Let the height of the tower is $h$ and $B C=x \mathrm{~m}$ In $\triangle A B C$,

$\tan 30^{\circ}=\frac{A C}{B C}=\frac{h}{x}$

$\Rightarrow \quad \frac{1}{\sqrt{3}}=\frac{h}{x}$ ......(i)

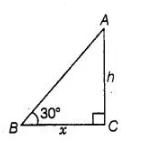
Case II By condition, the height of the tower is doubled. i.e., $P R=2 h$.

In $\triangle P Q R, \quad \tan \theta=\frac{P R}{Q R}=\frac{2 h}{x}$

$\Rightarrow \quad \tan \theta=\frac{2}{x} \times \frac{x}{\sqrt{3}}$  $\left[\because h=\frac{x}{\sqrt{3}}\right.$, from Eq. (i) $]$

$\Rightarrow \quad \tan \theta=\frac{2}{\sqrt{3}}=1.15$

$\therefore \quad \theta=\tan ^{-1}(1.15)<60^{\circ}$

Hence, the required angle is not doubled.