The angle of elevation of the top of a vertical tower PQ from a point X

Let PQ be the tower of height H m and an angle of elevation of the top of tower PQ from point X is 60°. Angle of elevation at 40 m vertical from point X is 45°.

Let PQ = H m and SX = 40m. OX = x, ,.

Here we have to find height of tower.

The corresponding figure is as follows

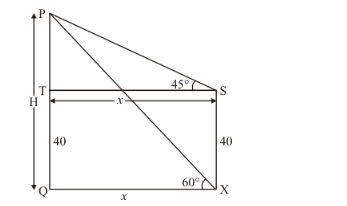
We use trigonometric ratios.

In

$\Rightarrow \quad \tan 45^{\circ}=\frac{h}{x}$

$\Rightarrow \quad 1=\frac{h}{x}$

$\Rightarrow \quad x=h$

Again in,

$\Rightarrow \quad \tan 60^{\circ}=\frac{h+40}{x}$

$\Rightarrow \quad \sqrt{3}=\frac{h+40}{x}$

$\Rightarrow \quad h+40=\sqrt{3} h$

$\Rightarrow h(\sqrt{3}-1)=40$

$\Rightarrow \quad h=\frac{40}{\sqrt{3}-1}$

$\Rightarrow \quad h=54.64$

Therefore $H=54.64+40$

$\Rightarrow H=94.64$

Hence the height of tower is $94.64 \mathrm{~m}$