The angle of elevation of the top of the building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°.

$\mathrm{PQ}=50$ metres is the height of the tower. Let $\mathrm{AB}=\mathrm{h}$ metres be the height of the building. Angle of elevation of the top of the building from the foot of the tower $=30^{\circ}$, i.e., $\angle \mathrm{AQB}=30^{\circ}$.

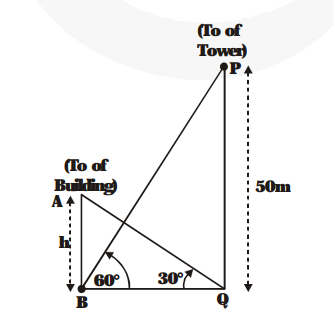
Angle of elevation of the top of the tower from the foot of the building

$=60$, i.e., $\angle \mathrm{PBQ}=60$

From $\triangle \mathrm{AQB}$

$\frac{\mathbf{h}}{\mathbf{B Q}}=\tan 30^{\circ}=\frac{\mathbf{1}}{\sqrt{\mathbf{3}}}$

$\Rightarrow \mathrm{BQ}=\mathbf{h} \sqrt{\mathbf{3}}$  ...(1)

From $\Delta \mathrm{PBQ}$

$\frac{50}{B Q}=\tan C D^{\circ}=\sqrt{3}$

$\Rightarrow \mathrm{BQ}=\frac{\mathbf{5 0}}{\sqrt{\mathbf{3}}}$   ...(2)

From (1) and (2), we have $\mathbf{h} \sqrt{\mathbf{3}}=\frac{\mathbf{5 0}}{\sqrt{\mathbf{3}}}$

$\Rightarrow \mathrm{h}=\frac{\mathbf{5 0}}{\mathbf{3}} \mathbf{m}$ i.e., $\mathrm{h}=\mathbf{1 6} \frac{\mathbf{2}}{\mathbf{3}} \mathbf{m}$