Question:
The angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is 6m.
Solution:
Let 
be tower of height 
m and angle of elevation of the top of tower from two points are 
and 
Let, 
m and 
m and 
The corresponding figure is as follows
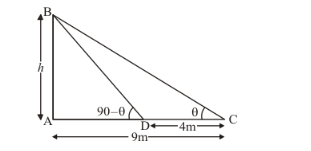
So we use trigonometric ratios.
In
,
$\Rightarrow \tan \theta=\frac{A B}{A C}$
$\Rightarrow \tan \theta=\frac{h}{4}$
Again in $\triangle A B D$,
$\Rightarrow \tan (90-\theta)=\frac{A B}{A D}$
$\Rightarrow \quad \tan \theta=\frac{9}{h}$
$\Rightarrow \quad \frac{h}{4}=\frac{9}{h}$
$\Rightarrow \quad h=6$
Hence the height of tower is $6 \mathrm{~m}$.