The aperture diameter of aelescope is $5 \mathrm{~m}$. The separation between the moon and the earth is $4 \times 10^{5} \mathrm{~km}$. With light of wavelength of $5500 A$, the minimum separation between objects on the surface of moon, so that they are just resolved, is close to:
Correct Option: 1
(1)
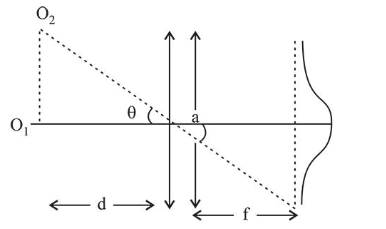
Smallest angular separation between two distant objects here moon and earth,
$\theta=1.22 \frac{\lambda}{a}$
$\mathrm{a}=$ aperture diameter of telescope
Distance $\mathrm{O}_{1} \mathrm{O}_{2}=(\theta) d$
Minimum separation between objects on the surface of moon,
$=\left(1.22 \frac{\lambda}{a}\right) d$
$=\frac{(1.22)\left(5500 \times 10^{-10}\right) \times 4 \times 10^{5} \times 10^{3}}{5}$
$=5368 \times 10^{-2} \mathrm{~m}=53.68 \mathrm{~m} \approx 60 \mathrm{~m}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.