Question:
The area (in sq. units) of the region $A=\left\{(x, y): x^{2} \leq y \leq x+2\right\}$ is:
Correct Option: , 2
Solution:
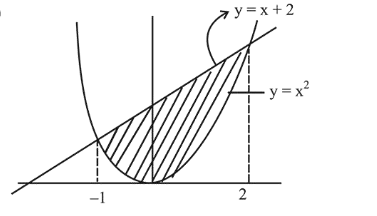
Required area is equal to the area under the curves $y \geq x^{2}$ and $y $\therefore$ requried area $\int_{-1}^{2}\left((x+2)-x^{2}\right) d x$ $=\left(\frac{x^{2}}{2}+2 x-\frac{x^{3}}{3}\right)_{-1}^{2}$ $=\left(2+4-\frac{8}{3}\right)-\left(+\frac{1}{2}-2+\frac{1}{3}\right)=\frac{9}{2}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.