Question:
The area (in sq. units) of the region
$\mathrm{A}=\left\{(x, \mathrm{y}): \frac{y^{2}}{2} \leq x \leq y+4\right\}$ is:
Correct Option: , 4
Solution:
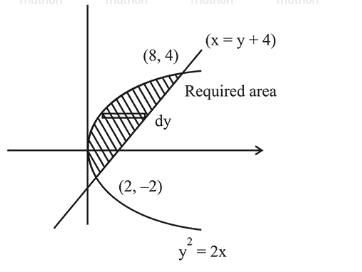
Given region, $A=\left\{(x, y): \frac{y^{2}}{2} \leq x \leq y+4\right\}$
Hence, area $=\int_{-2}^{4} x d y=\int_{-2}^{4}\left(y+4-\frac{y^{2}}{2}\right) d y$
$=\left[\frac{y^{2}}{2}+4 y-\frac{y^{3}}{6}\right]_{-2}^{4}=\left(8+16-\frac{64}{6}\right)-\left(2-8+\frac{8}{6}\right)$
$=\left(24-\frac{32}{3}\right)-\left(-6+\frac{4}{3}\right)=\frac{40}{3}+\frac{14}{3}=\frac{54}{3}=18$
