The area (in sq. units) of the smaller of the

The circle and parabola will have common tangent at $\mathrm{H}$ $(1,2)$.

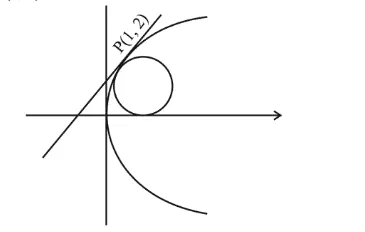
So, equation of tangent to parabola is,

$y \times(2)=\frac{4(x+1)}{2} \Rightarrow 2 y=2 x+2 \Rightarrow y=x+1$

Let equation of circle (by family of circles) is

$\left(x-x_{1}\right)^{2}+\left(y-y_{1}\right)^{2}+\lambda \mathrm{T}=0$

$\Rightarrow c \equiv(x-1)^{2}+(y-2)^{2}+\lambda(x-y+1)=0$

$\because$ circles touches $x$-axis.

$\therefore y$-coordinate of centre $=$ radius

$\Rightarrow c=x^{2}+y^{2}+(\lambda-2) x+(-\lambda-4) y+(\lambda+5)=0$

$\frac{\lambda+4}{2}=\sqrt{\left(\frac{\lambda-2}{2}\right)^{2}+\left(\frac{-\lambda-4}{2}\right)^{2}-(\lambda+5)}$

$\Rightarrow \frac{\lambda^{2}-4 \lambda+4}{4}=\lambda+5 \Rightarrow \lambda^{2}-4 \lambda+4=4 \lambda+20$

$\Rightarrow \lambda^{2}-8 \lambda-16=0 \Rightarrow \lambda=4 \pm 4 \sqrt{2}$

$\Rightarrow \lambda=4-4 \sqrt{2}(\because \lambda=4+4 \sqrt{2}$ forms bigger circle $)$

Hence, centre of circle $(2 \sqrt{2}-2,4-2 \sqrt{2})$ and radius

$=4-2 \sqrt{2}$

$\therefore$ area $=\pi(4-2 \sqrt{2})^{2}=8 \pi(3-2 \sqrt{2})$