The area of a circular path of uniform width h surrounding a circular region of radius r is

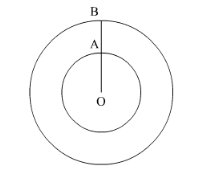
We have

$O A=r$

$A B=h$

Therefore, radius of the outer circle will be $r+h$.

Now we will find the area between the two circles.

Area of the circular path = area of the outer circle - area of the inner circle

$\therefore$ Area of the circular path $=\pi(r+h)^{2}-\pi r^{2}$

$\therefore$ Area of the circular path $=\pi\left(r^{2}+2 r h+h^{2}\right)-\pi r^{2}$

$\therefore$ Area of the circular path $=\pi\left(r^{2}+2 r h+h^{2}-r^{2}\right)$

Cancelling $r^{2}$ we get,

Area of the circular path $=\pi\left(2 r h+h^{2}\right)$

$\therefore$ Area of the circular path $=\pi(2 r+h) h$

Therefore, area of the circle is $\pi(2 r+h) h$.

Hence, the correct answer is option (b).