The area of a rhombus is 480 cm2, and one of its diagonals measures 48 cm.

It is given that,
Area of rhombus = 480 cm2.
One of the diagonal = 48 cm.

(i) Area of the rhombus $=\frac{1}{2} \times d_{1} \times d_{2}$

$\Rightarrow 480=\frac{1}{2} \times 48 \times d_{2}$

$\Rightarrow 480=24 \times d_{2}$

$\Rightarrow d_{2}=\frac{480}{24}$

$\Rightarrow d_{2}=20 \mathrm{~cm}$

$\Rightarrow 480=\frac{1}{2} \times 48 \times d_{2}$

$\Rightarrow 480=24 \times d_{2}$

$\Rightarrow d_{2}=\frac{480}{24}$

$\Rightarrow d_{2}=20 \mathrm{~cm}$

Hence, the length of the other diagonal is 20 cm.

(ii) We know that the diagonals of the rhombus bisect each other at right angles.

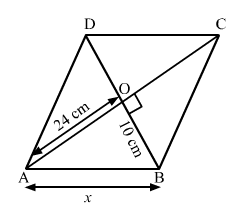
In right angled ∆ABO,

$A B^{2}=A O^{2}+O B^{2}$        (Pythagoras Theorem)

$\Rightarrow A B^{2}=24^{2}+10^{2}$

$\Rightarrow A B^{2}=576+100$

$\Rightarrow A B^{2}=676$

$\Rightarrow A B=26 \mathrm{~cm}$

Hence, the length of each of the sides of the rhombus is 26 cm.

(iii) Perimeter of the rhombus = 4 × side

= 4 × 26

= 104 cm

Hence, the perimeter of the rhombus is 104 cm.