The area of ∆AOB having vertices A(0, 6), O(0, 0) and B(6, 0) is

The points A(0, 6), O(0, 0) and B(6, 0) can be plotted on the Cartesian plane as follows:

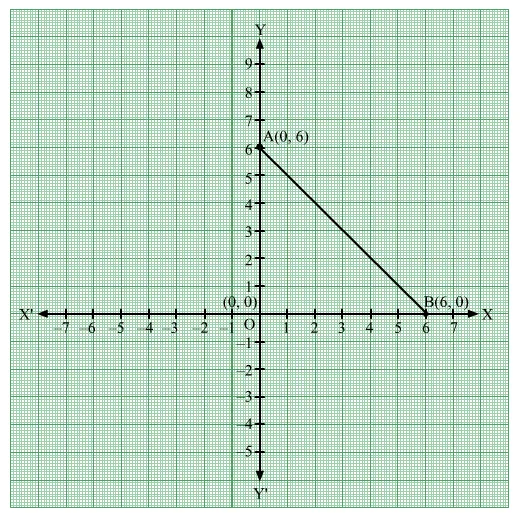
Here, ∆AOB is a right triangle right angled at O.

OA = 6 units and OB = 6 units

$\therefore$ Area of $\Delta \mathrm{AOB}=\frac{1}{2} \times \mathrm{OA} \times \mathrm{OB}=\frac{1}{2} \times 6 \times 6=18$ square units

Hence, the correct answer is option (c).