The area of incircle of an equilateral triangle is 154 cm2

Area of incircle of equilateral triangle is $154 \mathrm{~cm}^{2}$

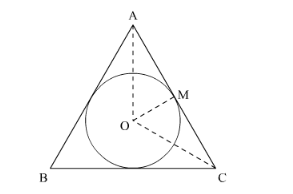
We have to find the perimeter of the triangle. So we will use area to get,

Area of incircle $=154$

$\pi r^{2}=154$

$r=\sqrt{\frac{154}{\pi}} \mathrm{cm}$

As triangle is equilateral so,

$\angle \mathrm{OCM}=30^{\circ}$

So,

$\tan 30^{\circ}=\frac{r}{\mathrm{MC}}$

$\mathrm{MC}=\sqrt{\frac{154(3)}{\pi}} \mathrm{cm}$

So,

$\mathrm{AC}=2(\mathrm{MC})$

$=2\left(\sqrt{\frac{154(3)}{\pi}}\right) \mathrm{cm}$

Therefore perimeter of the triangle is,

$=3(\mathrm{AC})$

$=6\left(\sqrt{\frac{462}{3.14}}\right)$

$=72.7 \mathrm{~cm}$

Therefore the answer is (d).