The area of the circle that can be inscribed

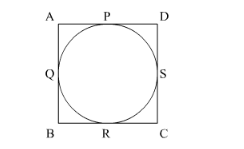
We know that ABCD is a square of length 10 cm. A circle is inscribed in the square therefore, all the sides of the square are become tangents of the circle.

By, the tangent property, we have

$A P=P D=5$

$A Q=Q B=5$

$B R=R C=5$

$C S=D S=5$

If we join PR then it will be the diameter of the circle of 10 cm.

Therefore, radius of the circle = 5cm

$\therefore$ Area of the circle $=\pi r^{2}$

$\therefore$ Area of the circle $=\pi \times 5^{2}$

$\therefore$ Area of the circle $=25 \pi$

Therefore, area of the circle is $25 \pi \mathrm{cm}^{2}$.

Hence, the correct answer is option $(d)$.