Question:
The area of the region, enclosed by the circle $x^{2}+y^{2}=2$ which is not common to the region bounded by the parabola $y^{2}=x$ and the straight line $y=x$, is:
Correct Option: , 4
Solution:
Total area - enclosed area between line and parabola
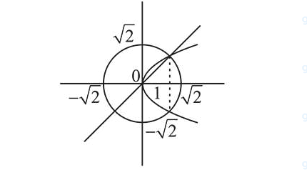
$=2 \pi-\int_{0}^{1} \sqrt{x}-x d x$
$=2 \pi-\left(\frac{2 x^{3 / 2}}{3}-\frac{x^{2}}{2}\right)_{0}^{1}$
$=2 \pi-\left(\frac{2}{3}-\frac{1}{2}\right)=2 \pi-\left(\frac{1}{6}\right)=\frac{12 \pi-1}{6}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.