Question:
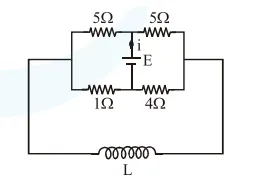
The current (i) at time $t=0$ and $t=\infty$ respectively for the given circuit is :
Correct Option: , 4
Solution:
At $\mathrm{t}=0$, current through inductor is zero,
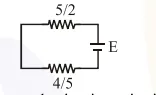
hence $\mathrm{R}_{\mathrm{eq}}=(5+1) \|(5+4)=\frac{18}{5}$
$i_{1}=\frac{E}{18 / 5}=\frac{5 E}{18}$
At $\mathrm{t}=\infty$, inductor becomes a simple wire and now the circuit will be as shown in figure
hence $\mathrm{R}_{\mathrm{eq}}=(5 \| 5)+(4 \| 1)=\frac{33}{10} ;(\| \Rightarrow$ parallel $)$
$\mathrm{i}_{2}=\frac{\mathrm{E}}{33 / 10}=\frac{10 \mathrm{E}}{33}$