The diameter of a coin is 1 cm (in the following figure).

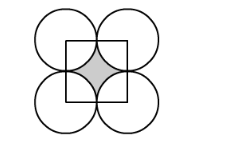
Look at the figure carefully shaded region is bounded between four sectors of the circle with same radius and a square of side 1 cm.

Therefore, the area of the shaded region is nothing but the difference the area of the square and area of one circle.

$\therefore$ Area of the shaded region $=$ Area of square $-$ Area of a circle

$\therefore$ Area of the shaded region $=1^{2}-\pi\left(0.5^{2}\right)$

$\therefore$ Area of the shaded region $=1-0.25 \pi$

Substituting $\pi=3.1416$ we get,

$\therefore$ Area of the shaded region $=1-3.1416 \times 0.25$

$\therefore$ Area of the shaded region $=1-0.7854$

$\therefore$ Area of the shaded region $=0.2146$

Therefore, area of the shaded region is $0.2146 \mathrm{~cm}^{2}$