The displacement time graph of a particle executing S.H.M. is given in figure : (sketch is schematic and not to scale)
The displacement time graph of a particle executing S.H.M. is given in figure : (sketch is schematic and not to scale)
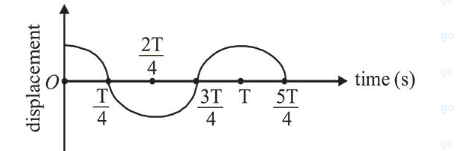
Which of the following statements is/are true for this motion?
(a) The force is zero at $t=\frac{3 T}{4}$
(b) The acceleration is maximum at $t=T$
(c) The speed is maximum at $t=\frac{T}{4}$
(d) The P.E. is equal to K.E. of the oscillation at $t=\frac{T}{2}$
Correct Option: , 3
(3) From graph equation of SHMv
$X=A \cos \omega t$
(a) At $\frac{3 T}{4}$ particle is at mean position.
$\therefore$ Acceleration $=0$, Force $=0$
(b) At $T$ particle again at extreme position so acceleration ismaximum.
(c) At $t=\frac{T}{4}$, particle is at mean position so velocity is
maximum.
Acceleration $=0$
(d) When $\mathrm{KE}=\mathrm{PE}$
$\Rightarrow \frac{1}{2} k\left(A^{2}-x^{2}\right)=\frac{1}{2} k x^{2}$
Here, $A=$ amplitude of SHM
$x=$ displacement from mean position
$\Rightarrow A^{2}=2 x^{2} \Rightarrow x=\frac{+A}{\sqrt{2}}$
$\Rightarrow \frac{A}{\sqrt{2}}=A \cos \omega t \quad \Rightarrow t=\frac{T}{2}$
$\therefore x=-A$ which is not possible
$\therefore A, B$ and $C$ are correct.
