The experimental data for decomposition of
$\left[2 \mathrm{~N}_{2} \mathrm{O}_{5} \longrightarrow 4 \mathrm{NO}_{2}+\mathrm{O}_{2}\right]$
in gas phase at 318K are given below:

(i) Plot [N2O5] against t.
(ii) Find the half-life period for the reaction.
(iii) Draw a graph between log [N2O5] and t.
(iv) What is the rate law?
(v) Calculate the rate constant.
(vi) Calculate the half-life period from k and compare it with (ii).
(i)
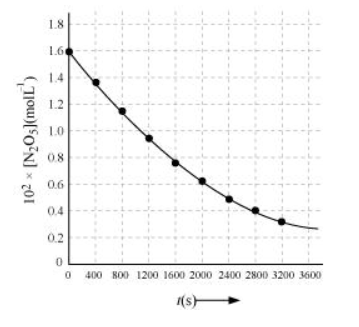
(ii) Time corresponding to the concentration, $\frac{1.630 \times 10^{2}}{2} \mathrm{~mol} \mathrm{~L}^{-1}=81.5 \mathrm{~mol} \mathrm{~L}^{-1}$, is the half life. From the graph, the half life is obtained as 1450s.
(iii)
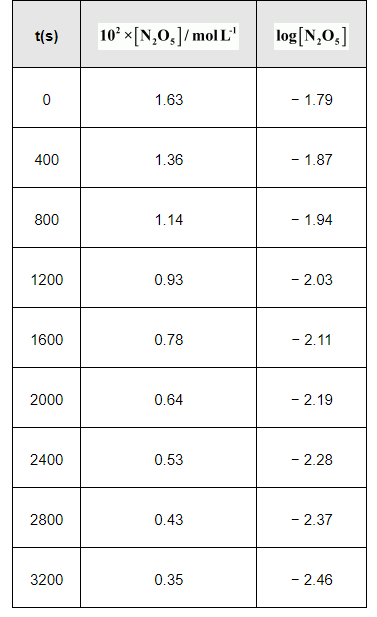
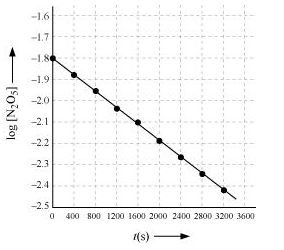
(iv) The given reaction is of the first order as the plot, $\log \left[\mathrm{N}_{2} \mathrm{O}_{5}\right] \mathrm{v} / \mathrm{s} t$, is a straight line. Therefore, the rate law of the reaction is
Rate $=k\left[\mathrm{~N}_{2} \mathrm{O}_{5}\right]$
(v) From the plot, $\log \left[\mathrm{N}_{2} \mathrm{O}_{5}\right] \mathrm{v} / \mathrm{s} t$, we obtain
Slope $=\frac{-2.46-(-1.79)}{3200-0}$
$=\frac{-0.67}{3200}$
Again, slope of the line of the plot $\log \left[\mathrm{N}_{2} \mathrm{O}_{5}\right] \mathrm{v} / \mathrm{s} t$ is given by
$-\frac{k}{2.303}$
Therefore, we obtain,
$-\frac{k}{2.303}=-\frac{0.67}{3200}$
$\Rightarrow k=4.82 \times 10^{-4} \mathrm{~s}^{-1}$
(vi) Half-life is given by,
$t_{1 / 2}=\frac{0.639}{k}$
$=\frac{0.693}{4.82 \times 10^{-4}} s$
$=1.438 \times 10^{3} s$
$=1438 s$
This value, 1438 s, is very close to the value that was obtained from the graph.
