The figure formed by joining the midpoints of the adjacent sides of a rectangle of sides 8 cm and 6 cm is a
Question:
The figure formed by joining the midpoints of the adjacent sides of a rectangle of sides 8 cm and 6 cm is a
(a) rectangle of area $24 \mathrm{~cm}^{2}$
(b) square of area $24 \mathrm{~cm}^{2}$
(c) trapezium of area $24 \mathrm{~cm}^{2}$
(d) rhombus of area $24 \mathrm{~cm}^{2}$
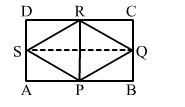
Solution:
(d) rhombus of $24 \mathrm{~cm}^{2}$
We know that the figure formed by joining the midpoints of the adjacent sides of a rectangle is a rhombus.
So, PQRS is a rhombus and SQ and PR are its diagonals.
i.e., SQ = 8 cm and PR = 6 cm
$\therefore \operatorname{ar}($ rhombus $P Q R S)=\frac{1}{2} \times$ product of diagonals $=\frac{1}{2} \times 8 \times 6=24 \mathrm{~cm}^{2}$
