The following table gives the frequency distribution of married women by age at marriage:
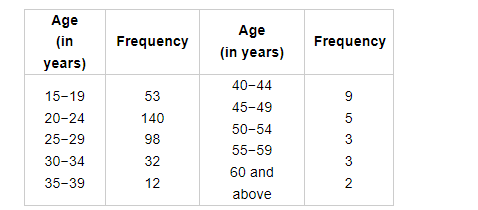
Calculate the median and interpret the results.
Here, the frequency table is given in inclusive form. So, we first transform it into exclusive form by subtracting and adding h/2 to the lower and upper limits respectively of each class, where h denotes the difference of lower limit of a class and upper limit of the previous class.
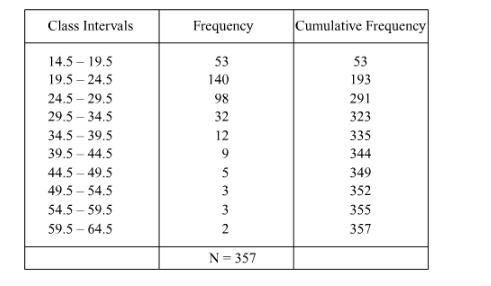
We have, N = 357
So, N/2 = 178.5
Thus, the cumulative frequency just greater than 178.5 is 193 and the corresponding class is 19.5−24.5.
Therefore, 19.5−24.5 is the median class.
Here, l = 19.5, f = 140, F = 193 and h = 5
We know that
Median $=l+\left\{\frac{\frac{N}{2}-F}{f}\right\} \times h$
$=19.5+\left(\frac{178.5-53}{140}\right) \times 5$
$=19.5+\frac{125.5}{140} \times 5$
$=19.5+\frac{125.5}{28}$
$=\frac{546+125.5}{28}$
$=23.98$
Hence, the median age 23.98 years.
Thus, nearly half the women were married between the age of 19.5 years and 24.5 years.
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
