The following table show the ages of the patients admitted in a hospital during a year:

Here, the maximum frequency is 23 so the modal class is 35−45.

Therefore,

$l=35$

$h=10$

$f=23$

$f_{1}=21$

$f_{2}=14$

$\Rightarrow$ Mode $=l+\frac{f-f_{1}}{2 f-f_{1}-f_{2}} \times h$

$=35+\frac{2}{46-35} \times 10$

$=35+\frac{2}{11} \times 10$

$=35+\frac{20}{11}$

$=35+1.80$

Mode $=36.8$ years

Thus, the mode of the ages of the patients is 36.8 years.

Calculation for mean.

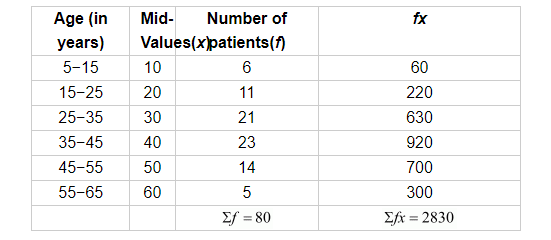
Mean $=\frac{\sum f x}{\sum f}=\frac{2830}{80}=35.37$

Thus, the mean age of the patients is 35.37 years.

The mean age of the patients is less than the modal age of the patients.