The foot of the perpendicular

Question:
The foot of the perpendicular drawn from the point $(4,2,3)$ to the line joining the points $(1,-2,3)$ and $(1,1,0)$ lies on the plane:

Correct Option: 1

Solution:

Equation of line through points $(1,-2,3)$ and $(1,1,0)$ is

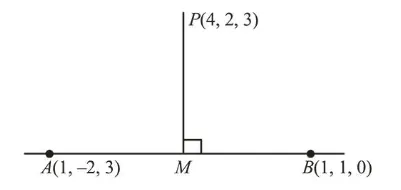
$\frac{x-1}{0}=\frac{y-1}{-3}=\frac{z-0}{3-0} \quad(=\lambda$ say $)$

$\therefore M(1,-\lambda+1, \lambda)$

Direction ratios of $\mathrm{PM}=[-3,-\lambda-1, \lambda-3]$

$\because P M \perp A B$

$\therefore(-3) \cdot 0+(-1-\lambda)(-1)+(\lambda-3) \cdot 1=0$

$\therefore \lambda=1$

$\therefore$ Foot of perpendicular $=(1,0,1)$

This point satisfy the plane $2 x+y-z=1$.