Question: The function, $f(x)=(3 x-7) x^{2 / 3}, x \in \mathbf{R}$, is increasing for all $x$ lying in :
(1) $(-\infty, 0) \cup\left(\frac{14}{15}, \infty\right)$
(2) $(-\infty, 0) \cup\left(\frac{3}{7}, \infty\right)$
(3) $\left(-\infty, \frac{14}{15}\right)$
(4) $\left(-\infty,-\frac{14}{15}\right) \cup(0, \infty)$
Correct Option: 1,
Solution:
$f(x)=(3 x-7) \cdot x^{2 / 3}$
$f^{\prime}(x)=3 x^{2 / 3}+(3 x-7) \cdot \frac{2}{3} x^{-1 / 3}$
$=\frac{15 x-14}{3 x^{1 / 3}}$
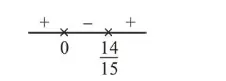
For increasing function