The function $f: A \rightarrow B$ defined by $f(x)=-x^{2}+6 x-8$ is a bijection if
(a) $A=(-\infty, 3]$ and $B=(-\infty, 1]$
(b) $A=[-3, \infty)$ and $B=(-\infty, 1]$
(c) $A=(-\infty, 3]$ and $B=[1, \infty)$
(d) $A=[3, \infty)$ and $B=[1, \infty)$
(a) $A=(-\infty, 3]$ and $B=(-\infty, 1]$
$f(x)=-x^{2}+6 x-8$, is a polynomial function
And the domain of polynomial function is real number.\
$\therefore x \in R$
$f(x)=-x^{2}+6 x-8$
$=-\left(x^{2}-6 x+8\right)$
$=-\left(x^{2}-6 x+9-1\right)$
$=-(x-3)^{2}+1$
Maximum value of $-(x-3)^{2}$ woud be 0
$\therefore$ Maximum value of $-(x-3)^{2}+1$ woud be 1
$\therefore f(x) \in(-\infty, 1]$
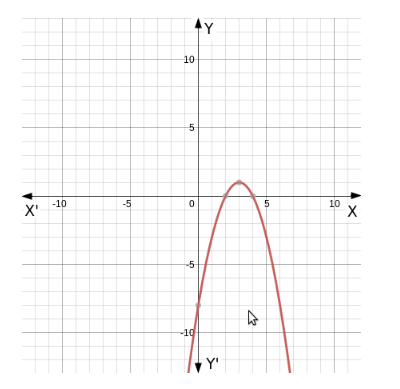
We can see from the given graph that function is symmetrical about $x=3$
\& the given function is bijective.
So, $x$ would be either $(-\infty, 3]$ or $[3, \infty)$
The correct option which satisfy A and B both is:
$A=(-\infty, 3]$ and $B=(-\infty, 1]$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.