The height of a solid cylinder is 15 cm

Solution:

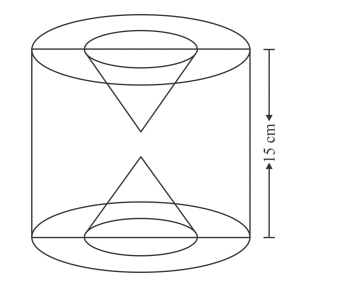
The height of cylinder h = 15 cm

Radius of cylinder $r=\frac{7}{2}$

The volume of cylinder

$=\pi r^{2} h$

$=\pi \times\left(\frac{7}{2}\right)^{2} \times 15 \mathrm{~cm}^{2}$

$=183.75 \pi$

The radius of conical holes = 3 cm

Height of conical holes = 4 cm.

The volume of conical holes

$=\frac{1}{3} \pi r^{2} h$

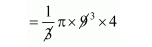
$=12 \pi \mathrm{cm}^{3}$

Clearly,

The volume of remaining solid

= vol. of cylinder − 2 × vol. of cone

$=183.75 \pi-24 \pi$

$=501.6 \mathrm{~cm}^{3}$