Question:
The height of an equilateral triangle having each side 12 cm, is
(a) $6 \sqrt{2} \mathrm{~cm}$
(b) $6 \sqrt{3} \mathrm{~cm}$
(c) $3 \sqrt{6} \mathrm{~cm}$
(d) $6 \sqrt{6} \mathrm{~cm}$
Solution:
(b) $6 \sqrt{3} \mathrm{~cm}$
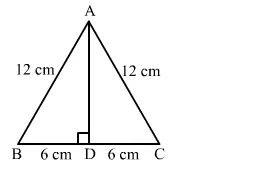
Let ABC be the equilateral triangle with AD as its altitude from A.
In right-angled triangle ABD, we have:
$A B^{2}=A D^{2}+B D^{2}$
$A D^{2}=A B^{2}-B D^{2}$
$=12^{2}-6^{2}$
$=144-36=108$
$A D=\sqrt{108}=6 \sqrt{3} \mathrm{~cm}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.