The horizontal distance between two poles is 15 m.

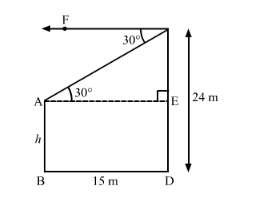
Let AB be the first pole and CD be the second pole.

Distance between the two poles, BD = 15 m

Height of the second pole, CD = 24 m

Suppose the height of the first pole be h m.

Draw AE ⊥ CD.

∴ CE = CD − ED = (24 − h) m                       [AB = ED = h m]

AE = BD = 15 m

Now, $\angle \mathrm{CAE}=\angle \mathrm{ACF}=30^{\circ}$ (Alternate angles)

In right $\triangle \mathrm{ACE}$,

$\tan 30^{\circ}=\frac{\mathrm{CE}}{\mathrm{AE}}$

$\Rightarrow \frac{1}{\sqrt{3}}=\frac{24-h}{15}$

$\Rightarrow \frac{15}{\sqrt{3}}=24-h$

$\Rightarrow h=24-5 \sqrt{3}$

$\Rightarrow h=24-5 \times 1.732=15.34 \mathrm{~m}$

Hence, the height of the first pole is 15.34 m.