The horizontal distance between two trees of different heights is 60 m.

Let the difference between two trees be DE = 60 m and angle of depression of the first tree from the top to the top of the second tree is.

Let BE = H m, AC = h m, AD = 80m.

We have to find the height of the first tree

The corresponding figure is as follows

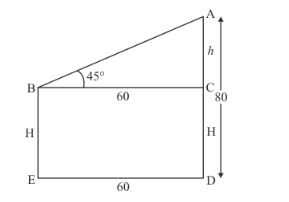
$\ln \triangle A B C$

$\Rightarrow \quad \tan B=\frac{A C}{B C}$

$\Rightarrow \quad \tan 45^{\circ}=\frac{h}{60}$

$\Rightarrow \quad 1=\frac{h}{60}$

$\Rightarrow \quad h=60$

Since $H=80-h$

$\Rightarrow \quad H=80-60$

$\Rightarrow \quad H=20$

Hence the height of first tree is $20 \mathrm{~m}$.