The inside perimeter of a running track (shown in the following figure) is 400 m.

It is given that, length of each straight portion $=90 \mathrm{~m}$ and width of track $=14 \mathrm{~m}$

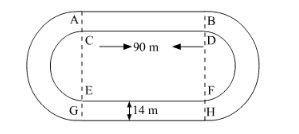
We know that the circumference C of semicircle of radius be r is

$C=\pi r$

The inside perimeter of running track is the sum of twice the length of straight portion and circumferences of semicircles. So,
inside perimeter of running track = 400 m

$2 l+2 \pi r=400 m$

$\Rightarrow 2 \times 90+2 \times \frac{22}{7} \times r=400 m$

$\Rightarrow r=\frac{220 \times 7}{2 \times 22}=35 \mathrm{~m}$

Thus, radius of inner semicircle is 35 m.

Now,

radius of outer semi circle r' = 35 + 14 = 49 m

Area of running track $=2 \times$ Area of rectangle $+2 \times$ Area of outer semi circle $-2 \times$ Area of inner semicircle

$=2 \times 90 \times 14+2 \times \frac{\pi(49)^{2}}{2}-2 \times \frac{\pi(35)^{2}}{2}$

$=2520+\pi \times(49+35)^{2}(49-35)$

$=2520+\frac{22}{7} \times 84 \times 14$

$=2520+3696=6216 m^{2}$

Hence, the area of running track $=6216 \mathrm{~m}^{2}$

Now, length L of outer running track is

$\mathrm{L}=2 \times 1+2 \pi r^{\prime}$

$=2 \times 90+2 \pi \times 49$

$=180+2 \times \frac{22}{7} \times 49$

$=180+308=488 m$

Hence, the length L of outer running track is 488 m.