The length of 40 leaves of a plant are measured correct to the nearest millimeter,

Calculation for mean.

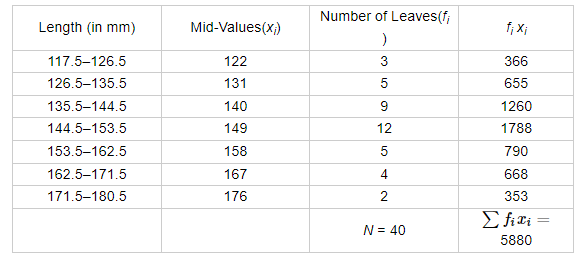
Mean length of the leaf $=\frac{1}{N} \sum f_{i} x_{i}=\frac{1}{40} \times 5880=147$

Calculation for median.

The given series is in inclusive form. Converting it to exclusive form and preparing the cumulative frequency table, we have

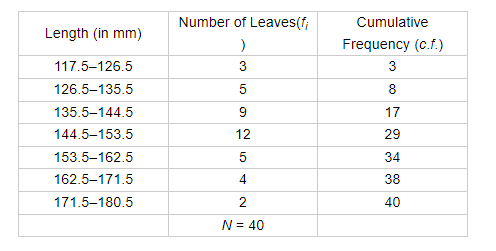
Now, we have

$N=40$

So, $\frac{N}{2}=20$

Now, the cumulative frequency just greater than 20 is 29 and the corresponding class is 144.5–153.5.

Therefore, 144.5–153.5 is the median class.

Here, $l=145, f=12, F=17$ and $h=7$

We know that

Median $=I+\left\{\frac{\frac{N}{2}-F}{f}\right\} \times h$

$=144.5+\left(\frac{20-17}{12}\right) \times 9$

$=144.5+\frac{27}{12}$

$=144.5+2.25$

$=146.75$

Hence, the median length of leaf is 146.75 mm.

Disclaimer: If the question asks for the mean length of the leaf, then the answer is 147 mm whereas if the question asks fro the median length of the leaf, then the answer is 146.75 mm, which is same as the answer given in the book.