The line segments joining the midpoints M and N of parallel sides AB and DC respectively of a trapezium ABCD is perpendicular to both the sides AB and DC.

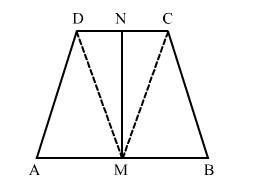
Given: In trapezium ABCD, M and N are mid-points of AB and DC, MN⊥">⊥⊥AB and MN⊥">⊥⊥DC.

To prove: AD = BC

Construction: Join CM and DM.

Proof:

In ΔCMN and ΔDMN,

MN = MN                           (Common sides)
∠">∠∠CNM = ∠">∠∠DNM = 90°">°°     (Given, MN⊥">⊥⊥DC)
CN = DN                             (Given, N is the mid-point DC)

∴">∴∴ By SAS congruence criteria,
ΔCMN ≅">≅≅ ΔDMN

So, CM = DM                  (CPCT)    .....(i)
And, ∠">∠∠CMN = ∠">∠∠DMN    (CPCT)
But, ∠">∠∠AMN = ∠">∠∠BMN = 90°">°°      (Given, MN⊥">⊥⊥AB)
⇒">⇒⇒∠">∠∠AMN -">−- ∠">∠∠CMN = ∠">∠∠BMN -">−- ∠">∠∠DMN
⇒">⇒⇒∠">∠∠AMD = ∠">∠∠BMC           .....(ii)

Now, in ΔAMD and ΔBMC,

DM = CM                            [From (i)]
∠">∠∠AMD = ∠">∠∠BMC                [From (ii)]
AM = BM                            (Given, M is the mid-point AB)

∴">∴∴ By SAS congruence criteria,
ΔAMD ≅">≅≅ ΔBMC

Hence, AD = BC    (CPCT)