Question:
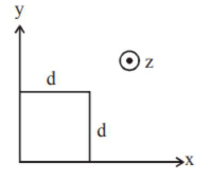
The magnetic field in a region is given by $\vec{B}=B_{0}\left(\frac{x}{a}\right) \hat{k}$. A square loop of side $\mathrm{d}$ is placed with its edges along the $x$ and $\mathrm{y}$ axes. The loop is moved with a constant velocity $\vec{v}=v_{0} \hat{i}$. The emf induced in the loop is :
Correct Option: 3,
Solution:
(3)
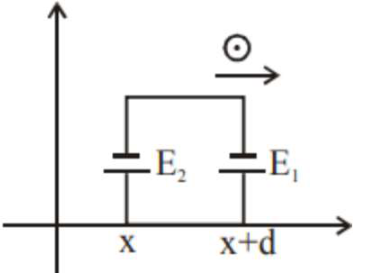
$\mathrm{E}_{1}=\frac{\mathrm{B}_{0}(\mathrm{x}+\mathrm{d})}{\mathrm{a}} \mathrm{v}_{0} \mathrm{~d}$
$\mathrm{E}_{2}=\frac{\mathrm{B}_{0}(\mathrm{x})}{\mathrm{a}} \mathrm{v}_{0} \mathrm{~d}$
$\mathrm{E}_{\text {net }}=\mathrm{E}_{1}-\mathrm{E}_{2}$
$\mathrm{E}_{\text {net }}=\frac{\mathrm{B}_{0} \mathrm{v}_{0} \mathrm{~d}^{2}}{\mathrm{a}}$