Question:
The mass of gas adsorbed, $x$, per unit mass of adsorbate, $m$, was measured at various pressures, $p$. A graph between $\log \frac{x}{m}$ and $\log p$ gives a straight line with slope equal to 2 and the intercept equal to $0.4771$. The value of $\frac{x}{m}$ at a pressure of $4 \mathrm{~atm}$ is : (Given $\log 3=0.4771$ )
Solution:
(6)
$\left(\frac{x}{m}\right)=k(p)^{\frac{1}{n}}$
$\log \left(\frac{x}{m}\right)=\log k+\frac{1}{n} \log p$
Slope $=\frac{1}{n}=2$, so $n=\frac{1}{2}$.
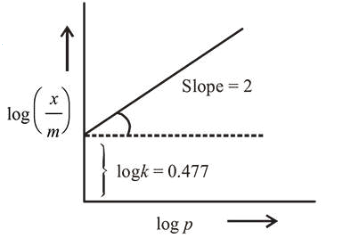
Intercept $\Rightarrow \log k=0.477$. So $k=$ Antilog $(0.477)=3$
So, $\left(\frac{x}{m}\right)=k(p)^{\frac{1}{n}}=3(4)^{\frac{1}{2}}=6$
