The midpoints of the sides AB, BC, CD and DA of a quadrilateral ABCD are joined to form a quadrilateral.

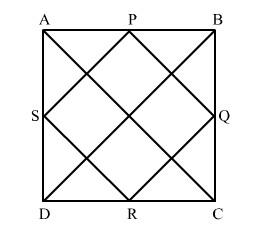
Given: In quadrilateral ABCD, AC = BD and AC ⊥ BD. P, Q, R and S are the mid-points of AB, BC, CD and AD, respectively.

To prove: PQRS is a square.

Construction: Join AC and BD.

Proof:

In ΔABC,

∵">∵∵ P and Q are mid-points of AB and BC, respectively.

$\therefore P Q \| A C$ and $P Q=\frac{1}{2} A C$   (Mid-point theorem)           ...(1)

Similarly, in ΔACD,

∵">∵∵ R and S are mid-points of sides CD and AD, respectively.

$\therefore S R \| A C$ and $S R=\frac{1}{2} A C$     (Mid-point theorem)          ...(2)

From (1) and (2), we get

PQ || SR and PQ = SR

But this a pair of opposite sides of the quadrilateral PQRS.

So, PQRS is parallelogram.

Now, in ΔBCD,

∵">∵∵ Q and R are mid-points of sides BC and CD, respectively.

$\therefore Q R \| B D$ and $Q R=\frac{1}{2} B D$       (Mid-point theorem)          ...(3)

From (2) and (3), we get

RS || AC and QR || BD

But, AC ⊥ BD                     (Given)

∴ RS ⊥ QR

But this a pair of adjacent sides of the parallelogram PQRS.

So, PQRS is a rectangle.

Again, AC = BD                (Given)

$\Rightarrow \frac{1}{2} A C=\frac{1}{2} B D$

⇒">⇒⇒ RS = QR                   [From (2) and (3)]

But this a pair of adjacent sides of the rectangle PQRS.

Hence, PQRS is a square.