The midpoints of the sides of a triangle along with any of the vertices as the fourth point makes a parallelogram of area equal to
The midpoints of the sides of a triangle along with any of the vertices as the fourth point makes a parallelogram of area equal to
(a) $\frac{1}{2}(\operatorname{ar} \Delta \mathrm{ABC})$
(b) $\frac{1}{3}($ ar $\Delta \mathrm{ABC})$
(c) $\frac{1}{4}($ ar $\Delta \mathrm{ABC})$
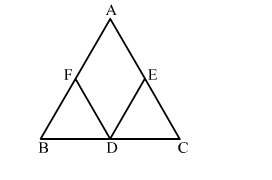
D, E and F are the midpoints of sides BC, AC and AB respectively.
On joining FE, we divide △ABC into 4 triangles of equal area.
Also, median of a triangle divides it into two triangles with equal area
$\operatorname{ar}(\mathrm{AFDE})=\operatorname{ar}(\triangle \mathrm{AFE})+\operatorname{ar}(\triangle \mathrm{FED})$
$=2 \operatorname{ar}(\triangle \mathrm{AFE})$
$=2 \times \frac{1}{4} \operatorname{ar}(\triangle \mathrm{ABC})=\frac{1}{2} \operatorname{ar}(\triangle \mathrm{ABC})$
Hence, the correct answer is option (a).
