Question:
The minimum value of $\alpha$ for which the equation $\frac{4}{\sin x}+\frac{1}{1-\sin x}=\alpha$ has at least one solution in $\left(0, \frac{\pi}{2}\right)$ is
Solution:
$f(x)=\frac{4}{\sin x}+\frac{1}{1-\sin x}$
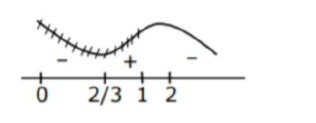
Let $\sin x=t \quad \because x \in\left(0, \frac{\pi}{2}\right) \Rightarrow 0 $f(t)=\frac{4}{t}+\frac{1}{1-t}$ $f^{\prime}(t)=\frac{-4}{t^{2}}+\frac{1}{(1-t)^{2}}$ $=\frac{t^{2}-4(1-t)^{2}}{t^{2}(1-t)^{2}}$ $=\frac{(t-2(1-t))(t+2(1-t))}{t^{2}(1-t)^{2}}$ $=\frac{(3 t-2)(2-t)}{t^{2}(1-t)^{2}}$ $f_{\min }$ at $t=\frac{2}{3}$ $\alpha_{\min }=f\left(\frac{2}{3}\right)=\frac{4}{\frac{2}{3}}+\frac{1}{1-\frac{2}{3}}$ $=6+3$ $=9$