The number of distinct real roots

Solution:

(b) 2

Let $\Delta=\mid \operatorname{cosec} x \quad \sec x \quad \sec x$

$\begin{array}{ccc}\sec x & \operatorname{cosec} x & \sec x \\ \sec x & \sec x & \operatorname{cosec} x\end{array}$

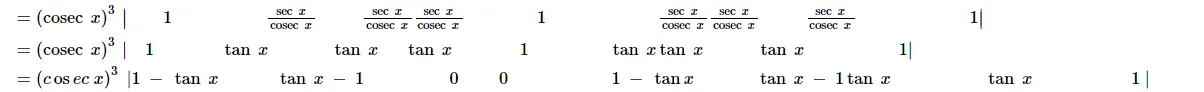
$\left[\right.$ Applying $\left.R_{1} \rightarrow R_{1}-R_{2}, R_{2} \rightarrow R_{2}-R_{3}\right]$

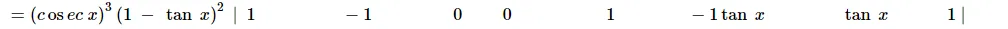
[Taking out $(1-\tan x)$ common from $R_{1}$ and $R_{2}$ ]

$=(\operatorname{cosec} x)^{3}(1-\tan x)^{2}\left\{1\left|\begin{array}{cr}1 & -1 \\ \tan x & 1\end{array}\right|+\tan x\left|\begin{array}{cc}-1 & 0 \\ 1 & -1\end{array}\right|\right\} \quad$ [Expanding along $C_{1}$ ]

$=(\operatorname{cosec} x)^{3}(1-\tan x)^{2}\{1+\tan x+\tan x\}$

$=(\operatorname{cosec} x)^{3}(1-\tan x)^{2}\{1+2 \tan x\}$

$\Delta=0$

$(c \operatorname{cosec} x)^{3}(1-\tan x)^{2}(1+2 \tan x)=0$

$\Rightarrow(1-\tan x)=0,(\operatorname{cosec} x)^{3}=0$ and $(1+2 \tan x)=0$

or

$\tan x=1, \operatorname{cosec} x=0$ and $\tan x=\frac{-1}{2}$

$\Rightarrow-\frac{\pi}{4} \leq x \leq \frac{\pi}{4} \quad\left[\tan x=1, \tan x=\frac{-1}{2}\right.$ are 2 real roots as cosec $x=0$ has no solution $]$

Thus, there are 2 solutions.