Question:
The number of distinct solutions of the equation, $\log _{1 / 2}|\sin x|=2-\log _{1 / 2}|\cos x|$ in the interval $[0,2 \pi]$, is_________.
Solution:
$\log _{1 / 2}|\sin x|=2-\log _{1 / 2}|\cos x|$
$\Rightarrow \log _{1 / 2}|\sin x \cos x|=2$
$\Rightarrow|\sin x \cos x|=\frac{1}{4}$
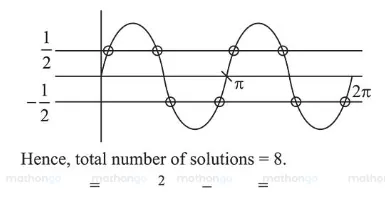
$\Rightarrow \quad \sin 2 x=\pm \frac{1}{2}$